2.3. Инвестирование в облигации

  ГЛОССАРИЙ

Купонная облигация – долговая ценная бумага, удостоверяющая право ее держателя на получение от лица, выпустившего облигацию, в предусмотренный ею срок номинальной стоимости облигации или иного имущественного эквивалента, а также периодических платежей в размере процентов от ее номинальной стоимости.

 Пример 7. Инвестор покупает облигацию компании Х по номиналу на первичном рынке со следующими эмиссионными параметрами: номинал облигации N=100000руб., купонная ставка 10% годовых от номинала, срок до погашения 3 года.

Итак, если инвестор, купив эту облигацию, не собирается ее перепродавать на вторичном рынке, то результатом его инвестиции будет:

А) через год компания обязана заплатить держателю облигации доход – купон (С) в размере:

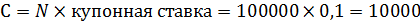
Б) еще через год компания обязана заплатить держателю облигации следующий купон С, т.е. еще 10тыс.руб.

В) и, наконец, в конце третьего года инвестор получит еще один купон и эмитент вернет держателю облигации 100тыс. руб., погасив облигацию по номиналу.

Итак, общая сумма, которую инвестор получит за три года составит:

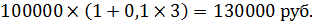
  Важно! В данном примере полученный результат инвестирования очень похож на традиционный депозитный вклад в коммерческий банк по схеме простых процентов.

Но рациональный инвестор постарается увеличить свой доход по максимуму и тогда получив очередной купонный платеж он не будет его тратить на текущие потребности, а может реинвестировать его на оставшийся срок до погашения облигации, например, положив его на депозитный вклад под банковский процент. Рассмотрим такое действие инвестора.

  Пусть ставка депозита равна 12% годовых. Тогда, получив через год купонную выплату в размере 10тыс. руб., инвестор положит его в банк на депозитный вклад на оставшиеся 2 года под 12% по схеме сложных процентов. Тогда к моменту погашения облигации на счете инвестора от этого купона накопится сумма:

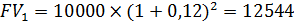
Еще через год следующий купон, который инвестор также положит в банк, но уже на оставшийся до погашения один год добавит на счет инвестора сумму:

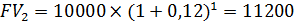
В итоге общая сумма, полученная инвестором от инвестиции в данную облигацию при погашении облигации по номиналу и выплате последнего третьего купона будет составлять:

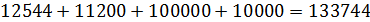
Вывод. Финансовый результат оказался выше, чем без реинвестирования купонных платежей.

  И, наконец, у владельца облигации есть еще другая интересная возможность! Ему не обязательно ждать момента погашения облигации. Он может свободно продать эту облигацию в любой момент на вторичном рынке ценных бумаг. Причем надо понимать, что продажа облигации на вторичном рынке уже происходит по некоторой рыночной цене, которая может отличаться от номинала и быть как ниже этого номинала так и выше.

Отсюда ставится важная практическая задача: а как правильно рассчитать эту рыночную стоимость облигации? И здесь нам вновь поможет финансовая математика.

Основой такого расчета является простая логика, что объективно инвестиция в облигацию должна дать такой же результат, как если бы инвестор вместо покупки облигации инвестировал такую же сумму на депозитный вклад в банк, зная годовую процентную ставка банка.

  Пример 8. Пусть наш инвестор, подержав облигацию у себя ровно год и получив купон в размере 10000 рублей принимает решение ее продать. Требуется рассчитать рыночную стоимость этой облигации при условии, что до погашения осталось ровно 2 года. Пусть годовая ставка депозитного вклада в банке равна 12%.

В решении такой задачи достаточно применить техникудисконтирования, выражающуюся в приведении будущей стоимости инвестиций к их текущей стоимости.

 Итак, этапы решения:

1. Сколько надо сегодня положить на счет в банк, чтобы через год на счете оказалась сумма равная второму купону по облигации? По формуле (7) подставив вместо FV величину купона C получим:

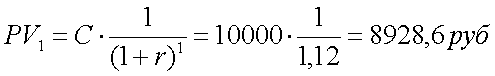
2. Сколько надо сегодня положить на счет в банк, чтобы через 2 года на счете оказалась сумма равная последнему купону и плюс номинал по облигации? По формуле (7) подставив вместо FV купон C+N получим:

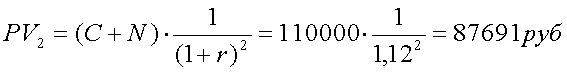
В итоге, потенциальный покупатель готов купить облигацию в условиях сложившихся в данный момент процентных банковских ставок по рыночной цене Р:

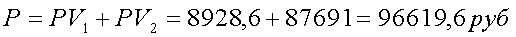
Выводы: если на рынке предлагается цена продажи данной облигации, например, 98000руб., то ее никто не купит, т.к. выгодней инвестировать такую сумму в банк. И наоборот, если выставляется цена, например, 95000руб., то,при прочих равных условиях, выгодно купить облигацию – она ниже расчетной!

К прочим равным условиям относится, в частности, оценка риска вложений в облигации данного эмитента. Если это государственные облигации или облигации компаний – лидеров рынка, то для оценки их стоимости можно использовать банковскую ставку процента по депозитам. В других случаях имеет смысл задуматься о риске банкротства компании, которая выпускает те или иные ценные бумаги.

Примечание. На практике купонные облигации могут быть и с различными купонными ставками в разных периодах. Впрочем, это не влияет на общую формулу для расчета текущей стоимости купонной облигации Pпри условии выплаты различных купонов Сiчерез равные промежутки времени в течении n лет до погашения ее по номиналу Nв конце срока можно использовать формулу:

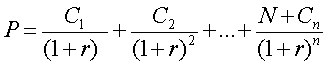
где

C1, c2, C3 – купоны, выплаченные в конце первого, второго, и т.д. периодов,

Сn – купон, выплаченный в конце при погашении,

r – доходность по альтернативному вложению.

Итак, мы можем теперь правильно рассчитать рыночную стоимость купонной облигации. Но это еще не все.

  Вопрос. Вот мы рассчитали рыночную стоимость облигации прямо на тот день, когда был выплачен очередной купон. А если покупать/продавать облигацию в периоды между выплатами купонов? Как справедливо разделить этот купон между покупателем и продавцом? Например, вы купили облигацию по расчетной рыночной цене в тот день, когда выплачивался купон и этот купон, конечно, забрал себе продавец. Теперь пошел срок вашего владения облигацией. Пусть прошло, например, сто дней, и вы принимаете решение продать облигацию. Купон эмитент вам через сто дней не будет выплачивать (купон обычно выплачивается раз в год или целыми периодами года, например, раз в полгода). Подсчитав стоимость облигации по стандартной формуле получается, что ее цена не изменилась. Значит, вы не имеете никакого дохода? Это несправедливо.

И тогда можно просто решить такую задачу – разделить годовой купон на две доли, где ваша доля будет часть купона за тот срок, который эта облигация вам принадлежала.

Другими словами, цена продажи/покупки облигации (так называемая полная цена Рп) складывается из расчетной (чистой) цены плюснакопленный купонный доход (НКД):

Pп = Р + НКД (накопленный купонный доход)

где НКД = C* Число дней (мес.), прошедших с момент выплаты очередного купона / база (365дн., 12 мес.)

  Пример 9. Чистая цена облигации с фиксированным купоном равна 894,40 рублей. Выплаты купонов производятся 1 раз в год, годовой купонный доход равен 280 рублей. Какую полную цену в рублях должен заплатить покупатель облигации, если со времени выплаты последнего купона прошло 78 дней? База: 365 дней в году.

Решение:

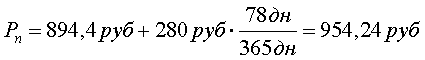
Доходность от инвестиции в облигации

Рассчитать доходность от инвестиции в облигацию не представляет никаких трудностей, пользуясь опять же аппаратом финансовой математики.

 Пример 10. Пусть инвестор купил облигацию по цене Р0 = 900 руб. и продал ее через месяц по цене Р1= 918 руб. Какова доходность в годовых от инвестиции в эту облигацию?

Рассчитаем сначала месячную доходность:

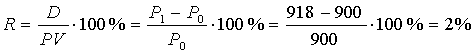
Тогда годовая доходность:
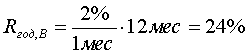